Voici mon TIPE, qui traite d’analyse d’image
numérique et de détection de contours.
¨Objectif
L’objectif du T.I.P.E. est d’étudier un nombre représentatif d’outils et de méthodes pour faire « parler » une image brute renvoyée par un satellite, en particulier la détection de contours.
¨Plan
I. Elément d’analyse d’images numériques
I.1
Cadre du TIPE
I.2
Présentation des images
I.3
L’histogramme : une abstraction de
l’espace
I.4
Notion d’analyse d’images
II. Méthodes statistiques
II.1
Seuillage
II.2
Classification d’image
II.3
Néocanaux
II.4
Histogrammes bidimensionnels
III. Analyse structurale : la détection de contours
III.1
Présentation de la détection de contours
III.2
Les transformations linéaires
III.3
La pratique et ses limites, l’extraction des réseaux fins
III.4
Utilisation pratique
Conclusion
Bibliographie
Annexes : A. Listing du programme de
calcul du Laplacien
B. Présentation du logiciel Imsat deluxe

Toutes les applications numériques et les images
finalisées sont obtenues avec le logiciel Imsat deluxe, que j’ai réalisé en
terminale avec un camarade ou avec un programme écrit en C.
I. Eléments d’analyse d’images numériques
I.1 Cadre du T.I.P.E.
Ce T.I.P.E. se propose de répondre à quelques questions concernant l’analyse des images spatiales.
· Quelle est la nature des images renvoyées par les satellites ?
· Comment extrait-on de cette image brute des données ?
· Peut-on mettre en évidence des structures particulières de l’image, telles que des routes, cours d’eau, parcelles de terre ?
On ne s’intéresse dans la chaîne de la télédétection qu’aux étapes de l’analyse de l’image brute. C’est-à-dire que la partie capteurs et mesure, bien qu’ayant fait l’objet d’une étude sommaire, ne rentre pas dans le cadre du T.I.P.E.
I .2 Notion d’image spatiale
On s’intéresse à des données collectées depuis l’espace représentant la variation spatiale d’une grandeur physique (ici amplitude d’une onde électro-magnétique) d’une portion de la terre. L’information est discrétisée et reçue sous forme d’une matrice de nombre de taille (n,m) où n et m sont le nombre de pixels de l’image-matrice, respectivement en longueur et en largeur.

Ordres de grandeur
Un pixel représente dans le cas de spot 1 une portion de 20m*20m, pour un satellite espion militaire la résolution et donc la taille des pixels atteint le mètre carré.
On se méprend souvent sur les images satellitaires. Plus que des simples photographies prises de l’espace, l’information qu’elles portent ne couvre pas seulement le domaine visible mais aussi des bandes de fréquence dans l’infrarouge, l’ultraviolet ou les ondes radar.
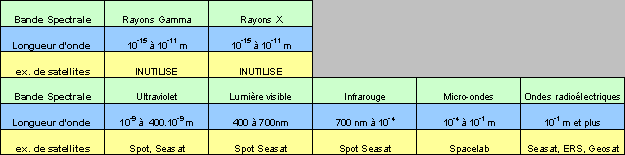
Tableau
1 : Spectre électro-magnétique
Toute la difficulté de l’analyse d’une image numérique réside justement dans l’association d’une couleur à une grandeur numérique, pour fournir une image exploitable par le plus puissant outil d’interprétation d’image connu à ce jour : l’œil humain.
Par ailleurs on conviendra d’appeler abusivement réflectance la grandeur contenue dans les images, sachant qu’en fait on mesure l’émittance + la réflectance des corps au sol.
I.3 Etude d’un exemple
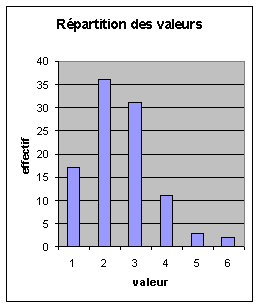
Prenons le cas de l’image-matrice suivante dont les valeurs R(n,m) sont dans {1 ;2 ;3 ;4 ;5 ;6} :
M :
On associe
aussi à une image son histogramme. Celui-ci
représente les effectifs correspondant à chaque réflectance. Il représente la
répartition des valeurs en faisant abstraction de la position des valeurs dans
l’image.
Pour obtenir une image à partir de la matrice une solution consiste à associer
une couleur à chaque réflectance, on obtient l’image :

On pourrait aussi associer aux valeurs {3,4,5,6} une seule couleur (par exemple si on sait que c’est de l’eau plus ou moins profonde) :

Dans la pratique on a plus de valeurs (256 pour une image spot) et des images qui ont plusieurs millions de pixels.
I.4 Notion d’analyse d’image
L’analyse d’image a pour but l’extraction de l’information caractéristique contenue dans une image. Celle-ci peut prendre la forme d’une image ou de toute autre structure de données permettant une description des entités contenues dans l’image. Essentiellement, l’analyse d’image fait appel à la segmentation où l’on va tenter d’associer à chaque pixel de l’image un label, en s’appuyant sur l’information portée et sa distribution spatiale dans l’image.
II Analyse statistique d’image.
Nous nous proposons
dans cette partie d’étudier quelques méthodes d’analyse d’image qui font appel
uniquement à l’information portée par chaque pixel, indépendamment de la
position de celui-ci.
II.1 Seuillage.
Plus généralement étant donné un histogramme on appelle seuillage les techniques consistant à segmenter une image en plusieurs classes.
Le plus souvent le seuillage consiste à associer à chaque pic de l’histogramme une classe. Il existe de très nombreuses méthodes de seuillage d’un histogramme. Ces méthodes s’appliquent correctement si l’histogramme contient réellement des pics assez distincts.
Il faut insister sur l’importance des
relevés sur le terrain qui seuls permettent de corroborer la pertinence de
l’analyse d’images.
Voici l’histogramme associé à une image spot de 576 lignes par 576 colonnes.
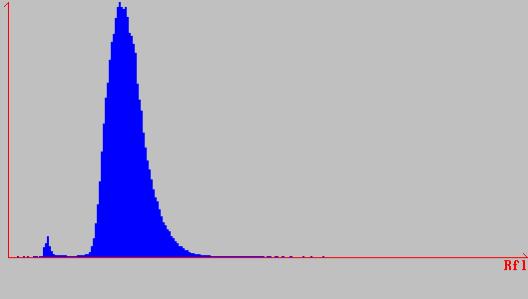
On reconnaît deux pics, le « gros » pic correspond à la végétation, le « petit » à une étendue d’eau (un lac).
Aussi est-il vraisemblable que l’utilisateur final désirera une image où l’étendue d’eau apparaîtra en bleu et la végétation en vert. On demande donc à un logiciel d’attribuer à la plage 0-60 du bleu, et au reste des nuances de vert. Une telle image serait :

Un mois après que cette image a été prise, il y a eu à l’est du lac un incendie de forêt, qui brûla la végétation. L’histogramme associé aux données que Spot renvoie est le suivant :
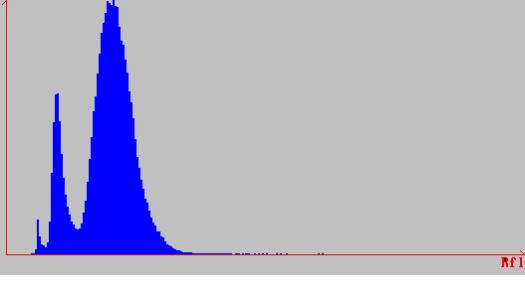
Il apparaît un troisième pic, qui correspond à la zone de forêt brûlée. L’image
avec les mêmes conventions de couleurs que précédemment plus la couleur rouge
pour le nouveau pic donne :

Cette méthode est on ne peut plus simple. Cependant dans la pratique des difficultés peuvent surgir. Si on veut comparer deux images prises par un satellite à deux saisons différentes il faudra tenir compte de la modification du feuillage de la végétation. De plus remarquons que les bords du lac apparaissent rouges : ils correspondent à la même réflectance que la zone brûlée. Les paragraphes suivants se proposent d’étudier quelques méthodes pour résoudre ce type de problème.
II.2 Classification d’images
La classification est un seuillage « amélioré ». Elle utilise plusieurs images. Soient I1,c I2,c … In,c n intervalles, pour chaque couleur c, On associe une couleur c à un couple v(x,y) si et seulement si v(x,y) est dans I1,cÇI2,cÇ…In,c.
La classification d’image permet d’extraire des informations de plusieurs images pour distinguer une entité particulière d’une image. Typiquement cette démarche répond à la question : que faire lorsqu’on veut séparer deux corps qui, pour une certaine bande de fréquence, renvoient les mêmes reflectances ?
Si l’on sait par exemple qu’une culture renvoie des valeurs de réflectance comprises entre 90 et 110 au début de l’été et entre 100 et 130 à la fin de l’été, alors on peut effectuer une classification d’images qui associera la couleur verte aux valeurs qui sont comprises entre 90 et 100 dans une image prise au début de l’été et comprises entre 100 et 130 à la fin de l’été. On élimine ainsi par exemple une culture parasite qui possède une réflectance entre 90 et 100 pendant toute la saison.
II.3 Néocanaux
Une image satellite traduit une grandeur physique. La nature de cette grandeur est variée. Radarsat envoie des données correspondant à des ondes radars. Spot émet des données sur plusieurs bandes de fréquence appelées canaux.
Un canal permet déjà de faire des observations importantes. Mais il est aussi possible d'utiliser les informations de plusieurs canaux simultanément. Des experts ont par exemple montré que le quotient (PIR-R)/(PIR+R) où « PIR » et « R » désignent des canaux de spots, était une bonne évaluation de la quantité de végétation. Les valeurs de l’image correspondront à l’indice de végétation.
Les néocanaux sont des canaux calculés en appliquant de telles formules.
II .4 Histogramme bidimensionnel
Il compte pour chaque couple (x,y) le nombre de points ayant la valeur de réflectance x dans le fichier X et la valeur y dans le fichier Y. Les points situés sur la diagonale principale (\) ont la même valeur, les points au-dessus ont une plus grande valeur dans X que dans Y, et ceux en dessous le contraire.

Exemple: indice de végétation[1] avant (X) et après (Y) un incendie. La petite tache en (60,60) représente un lac.
La grande tache de (130,130) à (200,200) représente les arbres qui n'ont pas brûlé.
La tache de (150,70) à (180,70) représente les arbres qui ont brûlé.
Les méthodes vues permettent, sans tenir
compte de la répartition spatiale des données, d’extraire une information
visuelle pertinente. L’objet de cette partie est de présenter une méthode pour
obtenir une image de contour, c’est-à-dire une image dans laquelle n’apparaît
plus que la frontière entre différents domaines de l’image.
Il y d’abord des méthodes de traitement
statistique, mais celles-ci peuvent faire intervenir des outils dont le niveau
dépasse largement les connaissances de classes préparatoires.
III Analyse structurale d’une image : détection de contour
Le but de cette partie est d’étudier un outil fondamental de l’analyse d’image : la détection de contour.
I.1 La détection de contour
La notion de contour est assez intuitive. Elle est fondée sur la capacité du système humain à distinguer plusieurs zones connexes d’aspect homogène, pour lesquelles la ligne de séparation sera appelée un contour ou une frontière. Il n’y a donc pas définition précise et on peut dire qu’il y a des contours là ou le système visuel humain en voit.
Intéressons nous à des contours du type marche d’escalier adoucie c’est-à-dire :

Dans le cas mono dimensionnel ces contours correspondent à des transitions du type :
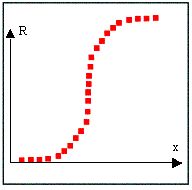
Un moyen pour mettre en évidence ce type de transition est de détecter l’inflexion, en détectant les passages à zéro de la dérivée seconde :
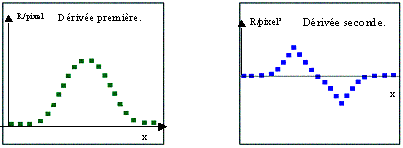
Dans le cas à deux dimensions, on calcule les passages à zéro du Laplacien. Dans la pratique de tels calculs sont fastidieux et gourmands en temps de calcul machine. L’idée pour simplifier les calculs est d’utiliser une transformation linéaire.
III.2 Les transformations linéaires.
a)
Présentation des
transformations linéaires
Soit une image matrice (R(m,n))m,n , on appelle transformation linéaire T une application de I dans I telle que:
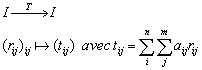
En fait, chaque pixel de l’image résultante est la somme pondérée de tous les
autres et de lui-même. Cependant pour la détection de contours il n’y que le
voisinage des points qui est intéressant. On se limite ainsi à des
transformations linéaires qui utilisent jusqu’à 8 pixels autour du pixel
considéré ou 24 :

L’application d’une transformation linéaire se résume donc à itérer sur chaque pixel une transformation locale, étape que l’on appelle masquage, de masque la matrice 3*3 ou 5*5 qui représentent les coefficients de la combinaison linéaire associée à chaque pixel. Par exemple la transformation linéaire « moyenne » qui homogénéise les pixels d’une image attribuerait au pixel central la somme de tous les coefficients du masque divisé par 9 :
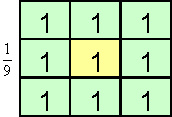
Dans toute la suite on convient ainsi de représenter un masque par une matrice,
la transformation de l’exemple précédent devient par exemple![]()
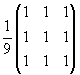 .
.
De plus, soit une image-matrice R on note M*R l’image obtenue en appliquant le masque M à l’image-matrice.
b) Retour à la détection de contour
On cherche donc une transformation linéaire sur un voisinage 3*3 qui modélisera le Laplacien discret en un point.
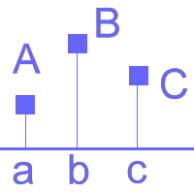
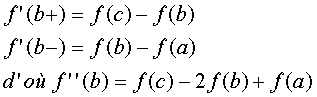
Par définition ![]() et on dispose de
trois points pour chaque direction. Trois points distincts étant donnés, la
meilleure approximation, à partir de ces trois points, de la dérivée seconde
est
et on dispose de
trois points pour chaque direction. Trois points distincts étant donnés, la
meilleure approximation, à partir de ces trois points, de la dérivée seconde
est ![]() qui s’explique par le
fait que, soient trois points
qui s’explique par le
fait que, soient trois points![]() A, B , C :
A, B , C :
En additionnant les dérivées secondes dans les deux directions x et y on obtient le masque M suivant :
![]()
![]()
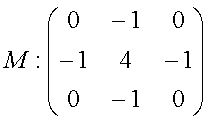
![]()
Pour obtenir enfin l’image des passages à zéros du Laplacien on effectue un traitement qui ne rentre pas dans le cadre du T.I.P.E. Mais qui se résume à distinguer positif et négatif , à dilater l’image et lui soustraire l’image originale.

c)Un mot sur la complexité
La complexité de notre algorithme est le temps de traitement d’un point i.e. du masquage local, multiplié par la dimension de l’image. Le masquage effectue (en prenant pour simplifier l’addition comme unité de temps calcul) 8 additions, donc la complexité est en 8 N².

III.3 La pratique et ses limites
Dans cette
partie où l’on teste l’efficacité de notre procédé, toutes les images sont
obtenues à l’aide d’un programme écrit en C, qui se trouve en annexe.
a)Un exemple idéal.
Voici par exemple un contour parfait pour notre méthode : un dégradé circulaire avec deux paliers bleu foncé et bleu turquoise (0 à 255) :
Et voici l’image du module
du laplacien (gris=0 vert=190), et voici l’image originale avec la ligne de
changement de signe mise en évidence en rouge :

b)Etude des contours « en toit »
Image idéale (échelle de gris 0-255)
Voici
maintenant un exemple qui illustre l’utilité du Laplacien pour détecter une
classe de contours particuliers : les routes et les cours d’eau. Soit
l’image idéale de routes ou de cours d’eau :
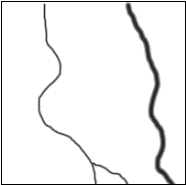
Le profil du contour est différent de ceux auxquels nous nous
intéressons, c’est un contour en toit :
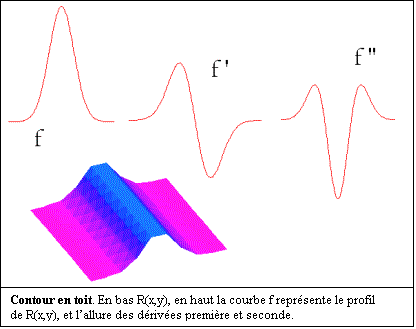
On peut se poser la question suivante : compte tenu de la dérivée
seconde qui est grande sur le contour, ne suffit-il pas de considérer l’image
du Laplacien, sans considérer ses passages à zéro ?
Dans un cas idéal, comme celui de notre image test, l’image du
Laplacien suffit :

On pourrait donc croire que le Laplacien donne directement ce genre de contours.
Il n’en est rien dans la pratique, pour preuve cet exemple :
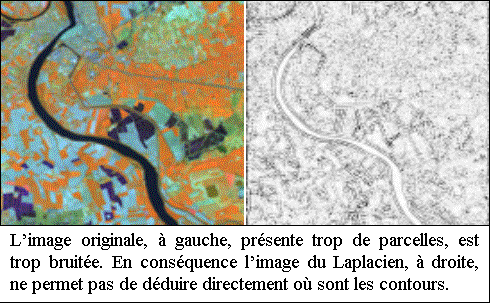
Notre procédé donne t-il des
résultats plus satisfaisants ? La pratique tend à le prouver (cf. infra),
en voici l’explication. Bien qu’extrémale sur le contour, la dérivée seconde s’annule
deux fois autour de l’extremum, ce double passage est bien détecté par notre
procédé. Le seul inconvénient est l’imprécision induite. Le contour est plus
« épais ».
Voici donc comme promis le
résultat de notre procédé sur l’image :
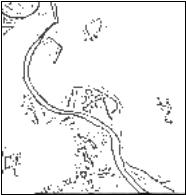
Il reste encore des zones
bruitées, mais on obtient bien le réseau fin principal.
Au prix d’une légère perte
de précision, notre procédé peut donc détecter ce qu’on appelle les réseaux
fins (contours en toit) : routes, réseaux ferroviaires, cours d’eau.
c)Un exemple et amélioration du procédé
Voici un exemple, dans la
région de la Crau :

Après détection de la ligne
de passage à zéro du Laplacien :
Image finale des contours

Il faut remarquer le
dédoublement des lignes du passage à zéro entre deux zones homogènes.
L’image finale comme
l’image obtenue en b) met en évidence une limitation de notre procédure :
le passage à zéro est une condition nécessaire mais pas suffisante de détection
d’un contour. Il reste sur l’image finale des contours parasites qui ne
correspondent pas forcément aux contours francs que l’on cherche. Ici on
obtient aussi des contours en « pente douce ». La solution partielle
que m’a proposée un spécialiste du sujet est de calculer aussi l’image du
module du vecteur gradient à l’aide encore une fois d’un opérateur de
masquage local.
En combinant passage à zéro
du Laplacien et présence d’un fort gradient, on élimine bon nombre d’entités
engendrant la détection d’un contour. Cependant il reste un problème majeur,
commun à toutes les techniques de traitement d’un signal : le bruit.
d)Une autre limite importante : le bruit
En pratique la méthode de
détection des contours par passage à zéro du Laplacien n’est efficace que
lorsque l’image n’est pas bruitée. En effet, une analyse fréquentielle montre
que le Laplacien possède un caractère passe-haut qui amplifie le bruit.
Les images à analyser sont en effet souvent bruitées c’est à dire qu’elles présentent de nombreuses discontinuités locales parasites. Il est donc nécessaire bien souvent avant de générer l’image du module du Laplacien d’utiliser un filtrage passe-bas sur l’image pour éradiquer les contours parasites.
Le passe bas le plus simple peut être modélisé par le masque « moyenne » vu précédemment. En fait le masque rend l’image légèrement floue, ce qui absorbe les points parasites et homogénéise les textures. La page suivante illustre l’intérêt d’un tel filtrage.
III.4 Utilisation pratique
La détection de contours joue un rôle
particulièrement important dans l’analyse d’image.
· La détection de contours
est la première étape pour l’extraction des réseaux routiers, ferroviaires
et fluviaux.
· La détection de contours
est utile pour le cadastre, elle met généralement bien en valeur les parcelles
de terrain.
·Elle intervient
indirectement dans d’autres techniques d’analyse d’images car elle met bien en
évidence la structure d’une image.
Conclusion : procédé de détection des contours
Forts des essais sur des images réelles, la méthode de détection de contours que nous avons établie est la suivante :
· Application d’un filtrage type passe-bas
· Calcul à l’aide d’un opérateur de masquage local de l’image du module du Laplacien
· Création de l’image des passages à zéro du Laplacien : I
(·) Calcul à l’aide d’un opérateur de masquage local de l’image du module du vecteur gradient : G
· Seuillage de l’image I à partir des données de l’image G : au delà d’une certaine valeur de G(n,m) on considère que le point I(n,m) peut être un contour.
Conclusion
Maillon final de la télédétection, l’analyse d’images se doit de corriger les faiblesses des maillons précédents et de fournir le produit final à l’utilisateur : une image dans laquelle apparaît seulement l’information utile.
Les techniques mises en œuvre pour la télédétection sont nombreuses et la tâche la plus difficile de l’ingénieur en charge de l’analyse d’images est de choisir une technique adaptée. Comme nous l’avons souligné pour la détection des contours, il n’existe pas une méthode unique, mais un panel de méthodes adaptées à chaque cas. Les recherches actuelles dans ce domaine portent justement sur des procédés qui permettraient d’automatiser ce choix, ensemble de procédés appelé pilotage par l’applicatif.
Références bibliographiques et URL internet
[1] Traitement numérique des images, sous la direction de Murat Kunt, presses polytechniques et universitaires romandes.
[2] Article télédétection de l’Encyclopaedia Universalis.
[3] Segmentation d’image où en somme nous ? Olivier Monga, rapport de recherche n°1216 de l’INRIA, unité de recherche INRIA-ROCQENCOURT
[4]L’observation de la terre par les satellites, Fernand Verger, PUF.
[5]www-projet.cnes.fr :8090/segmentation/menu.html
[6]www-ima.enst.fr/~maitre/BETI